In terms of natural or environmental risk management, analysing uncertainties is an essential decision-making step. There are two sources of uncertainty:
- The first source results from the natural variability of the modelled phenomena: this uncertainty is referred to as “random”. This first source can be modelled in detail using probability-based tools.
- The second source, referred to as “epistemic”, appears in the presence of “imprecise, vague or even incomplete” information, i.e. this uncertainty is linked to our lack of knowledge of phenomena and appears every time the input data are too limited (quality and quantity). Typically, the following case frequently occurs: due to study costs and deadlines, only a small number of values of a parameter can be obtained (this situation is referred to as “partial ignorance”).
When confronted with epistemic uncertainty, “conventional” probability theory tools frequently appear too restrictive. Other, more flexible representation tools can then be put forward (intervals, fuzzy numbers, parametric probability categories, etc.).
With this in mind, BRGM has developed methods/tools in close cooperation with IRIT to manage representations of uncertainties in relation to groundwater. For this purpose, the HYRISK package was developed in free R software. This propagates and uses random uncertainties (represented by probabilities) and epistemic uncertainties (represented by intervals, fuzzy numbers or parametric probability categories) together. It extends the functionality of the excel tutorial with the same name.
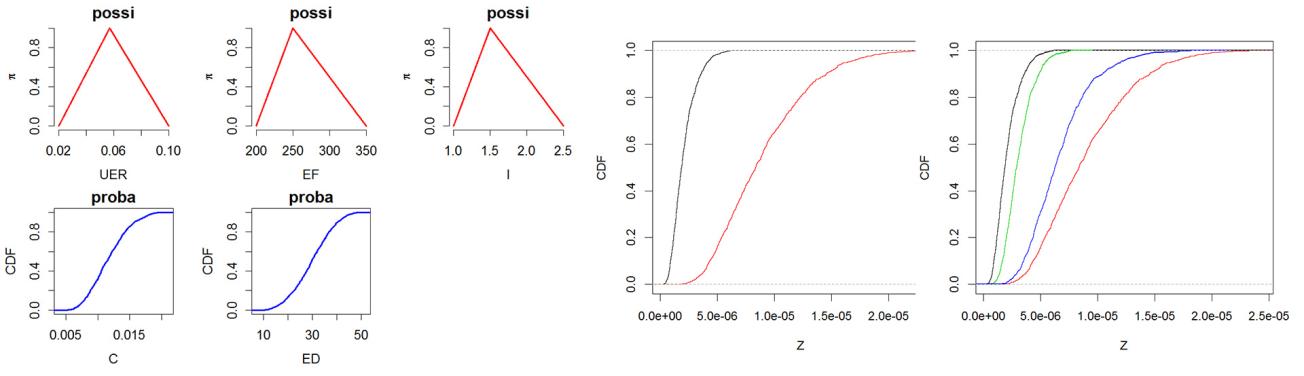
Graphs produced with Hyrisk software.
© BRGM
Functionality of the R HYRISK package
The R HYRISK package easily carries out the following operations:
- Representation of uncertain variables in different forms: probability distributions (Normal, log-Normal, triangular, Gumbel, beta or defined by the user), intervals, fuzzy numbers (triangular or trapezoidal), categories of parametric probability distributions, i.e. probability distributions with imprecise parameters (e.g. normal distribution with average and variance represented by intervals);
- Propagation of uncertainties using the IRS algorithm of Baudrit et al. (2007) or the Hydride algorithm described by Baudrit et al., (2006);
- Sensitivity analysis using a pinching approach (Ferson and Tucker, 2006);
- Summary of the results of propagation to help with decision-making, in the form of a cumulative probability distribution pair, a single distribution taking risk aversion into account (Dubois and Guyonnet 2011), an exceedance probability interval and a quantile interval.
References
In English
- Baudrit, C., Dubois, D., & Guyonnet, D. 2006. Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment. IEEE transactions on fuzzy systems, 14(5), 593-608.
- Baudrit, C., Guyonnet, D., Dubois, D. 2007. Joint propagation of variability and partial ignorance in a groundwater risk assessment. Journal of Contaminant Hydrology, 93: 72-84.
- Dubois D., Guyonnet D. 2011. Risk-informed decision making under epistemic uncertainty. International Journal of General Systems, 40(2), 145-167.
- Ferson, S., & Tucker, W. T. (2006). Sensitivity analysis using probability bounding. Reliability Engineering & System Safety, 91(10), 1435-1442.
In French
Free licensing available
The R HYRISK package can be downloaded free of charge for Windows XP, 7, 8 or 10 and for UNIX under CRAN. The software will run on both 32-bit and 64-bit machines.







From left to right: 1. Representation of uncertain inputs in the health risk assessment model related to the exposure of people to an organochlorine solvent (1,1,2 trichloroethane) from consuming contaminated water (described by Dubois and Guyonnet, 2011). Imprecise variables represented by triangular fuzzy numbers are marked in red; random variables represented by probability distributions are marked in blue. 2. Example of the result of propagating random and epistemic uncertainties using the IRS algorithm (Baudrit et al., 2007) following the example of the health risk model described by Dubois and Guyonnet (2011). 3. Example of a result of “pinching” that involves reducing the lack of precision of an imprecise variable by fixing it to a single value. The result of propagation, taking all uncertainties into account, is marked in black and red; the result of propagation after eliminating the lack of precision of a parameter is marked in green and blue.