En matière de gestion des risques (naturels ou environnementaux), l’analyse des incertitudes est une étape essentielle pour aider à la prise de décision. Deux types de sources d’incertitudes existent :
- La première source résulte de la variabilité naturelle des phénomènes modélisés : c’est l’incertitude dite "aléatoire". Cette première source peut être rigoureusement modélisée par les outils probabilistes.
- La seconde source dite "épistémique" apparaît lorsqu’on est en présence d’une information "imprécise, vague voire incomplète", c'est-à-dire que cette incertitude est liée à notre méconnaissance de phénomènes et apparaît chaque fois que les données d’entrée sont trop limitées (qualité et quantité). Typiquement, on est souvent confronté au cas suivant : les coûts et délais d’étude ne permettent d’obtenir qu’un nombre épars de valeurs d’un paramètre (situation dite "d’ignorance partielle").
Face à l’incertitude épistémique, les outils "classiques" de la théorie des probabilités apparaissent souvent trop contraignants. D’autres outils de représentation plus flexibles peuvent alors être proposés (intervalles, nombres flous, familles de probabilités paramétriques etc.).
C’est dans cette optique que le BRGM en collaboration étroite avec IRIT a développé des méthodes / outils pour gérer des représentations hydriques des incertitudes. Dans ce but, le package HYRISK a été développé dans le logiciel libre R. Il permet la propagation et l’exploitation conjointe des incertitudes aléatoires (représentées par des probabilités) et épistémiques (représentées par des intervalles ou des nombres flous ou des familles de probabilités paramétriques). Il étend les fonctionnalités du didacticiel excel du même nom.
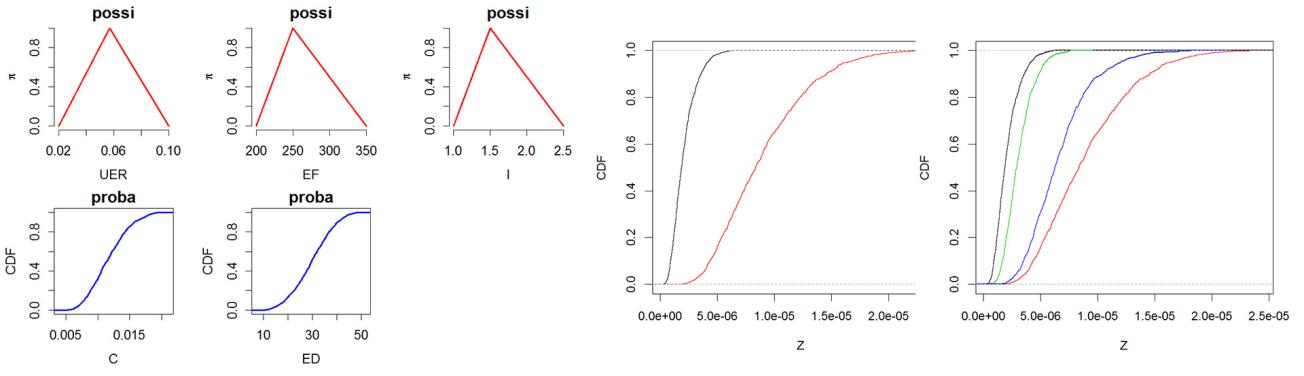
Graphes produits avec le logiciel Hyrisk.
© BRGM
Fonctionnalités du package R HYRISK
Le package R HYRISK permet de réaliser simplement les opérations suivantes :
- Représenter des variables incertaines sous différentes formes: lois de probabilités (Normal, log-Normal, triangulaire, Gumbel, beta ou défini par l’utilisateur), intervalles, nombres flou (triangulaire ou trapézoïdal), famille de lois de probabilités paramétriques i.e. des lois de probabilités avec paramètres imprécis (e.g. loi normale avec moyenne et variance représentées par des intervalles);
- Propager les incertitudes à l’aide de l’algorithme IRS de Baudrit et al. (2007) ou celui Hydride décrit dans par Baudrit et al., (2006);
- D’analyser la sensibilité par une approche "pinching" (Ferson and Tucker, 2006) ;
- Synthétiser les résultats de la propagation pour une aide à la décision, sous la forme d’une paire de distribution de probabilités cumulées, d’une distribution unique prenant en compte l’aversion au risque (Dubois et Guyonnet 2011), d’un intervalle de probabilités de dépassement et d’un intervalle de quantile.
Références
En anglais
- Baudrit, C., Dubois, D., & Guyonnet, D. 2006. Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment. IEEE transactions on fuzzy systems, 14(5), 593-608.
- Baudrit, C., Guyonnet, D., Dubois, D. 2007. Joint propagation of variability and partial ignorance in a groundwater risk assessment. Journal of Contaminant Hydrology, 93: 72-84.
- Dubois D., Guyonnet D. 2011. Risk-informed decision-making under epistemic uncertainty. International Journal of General Systems, 40(2), 145-167.
- Ferson, S., & Tucker, W. T. (2006). Sensitivity analysis using probability bounding. Reliability Engineering & System Safety, 91(10), 1435-1442.
En français
Mise à disposition de licences d’utilisation gratuite
Il est possible télécharger gratuitement le package R HYRISK pour une utilisation sous Windows XP, 7, 8 ou 10 ainsi que UNIX sous le CRAN. Le logiciel fonctionne indifféremment sur les machines 32 bits ou 64 bits.







De gauche à droite : 1. Représentation des entrées incertaines du modèle d’évaluation du risque sanitaire lié à l’exposition de personnes à un solvant organochloré (du 1,1,2 trichloroéthane) par le biais de la consommation d’eau polluée (décrit par Dubois et Guyonnet, 2011). En rouge, les variables imprécises représentées par des nombres flous triangulaires ; En bleu les variables aléatoires représentées par des lois de probabilités. 2. Exemple de résultat de propagation des incertitudes aléatoires et épistémiques à l’aide de l’algorithme IRS (Baudrit et al., 2007) sur l’exemple du modèle de risque sanitaire décrit par Dubois et Guyonnet (2011). 3. Exemple de résultat d’un "pinching" consistant à réduire l’imprécision sur une variable imprécise en la fixant à une valeur unique. En noir et rouge, le résultat de la propagation en tenant compte de l’ensemble des incertitudes ; En vert et bleu, le résultat de la propagation après avoir enlevé l’imprécision sur un paramètre.